Ohm :
_____________________________________________________________________
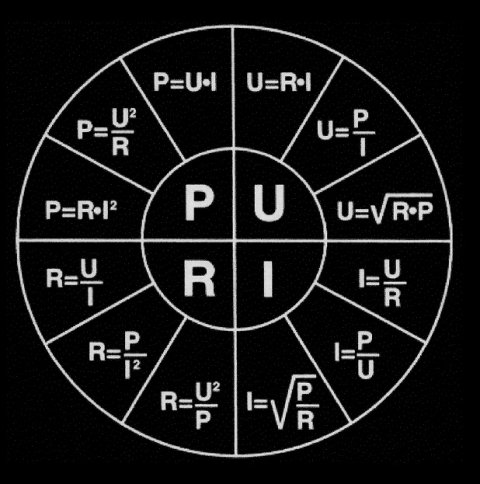
Ohm`s lov :
P = Effekt (Watt)
U = Spænding (Volt)
I = Strømstyrke (Ampere)
R= Modstand (Ohm)
_____________________________________________________________________
Oktav : Se "Pink noise".
_______________________________________________________________________
Overtoner : Når man hører en enkelt tone hører man i virkeligheden mange toner, idet den enkelte tone indeholder overtoner. En tone helt uden overtoner kaldes en sinustone. Næsten alle musikalske lyde er sammensat af mange sinustoner - hvor mange og med hvilke talforhold og styrkeforhold imellem dem er afgørende for klangfarven. I slagtøjslyde, som f. eks et bækkenslag, er der ikke noget simpelt talforhold mellem overtonerne, men i en orgeltone eller en violintone er der et simpelt talforhold mellem alle overtonerne.
Grundtonen i klangen kaldes 1. deltone, 1. overtone kaldes for 2. deltone etc. Forholdet mellem deltonerne er: 1 : 2 : 3 : 4 : 5 : 6 : 7 : 8 ... Dette kaldes for en harmonisk serie. Harmonisk serie Det dybe G har et svingningstal på (ret præcist) 49 Hz. Det betyder, at overtonerne til denne tone er på 98, 147, 196, 245 etc. Disse toner er vist i nodeeksemplet:

Ligesvævende temperatur Imidlertid rammer overtonerne ikke helt præcis tonerne på et klaver (der er stemt i ligesvævende), nogle af dem afviger temmelig meget. Afvigelsen er sat op cents, dvs. hundrededele af en halvtone. 50 cent er altså en kvart tone. Overtonerækkens intervaller er rene Alle intervallerne i overtonerækken er fuldstændig eksakt rene - den rene kvint har eksakt talforholdet 2:3, den rene terts har eksakt talforholdet 4:5. I overtonerækken afviger kvinten G med +2 cent, dvs. overtonen er lidt højere end klaverets kvint, der altså egentlig er lidt for lav. Den store terts er hele 14 cent lavere end klaverets terts - vi har altså vænnet os til at det store tertser på klaveret er en hel del for store. "Naturseptimen" med talforholdet 4:7 er ca. en tredjedel af en halvtone lavere end klaverets septim. Overtonerækken indeholder en durtreklang med deltone 1, 3 og 5 (eller 3, 4 og 5) - ifølge sagens natur fuldstændigt ren. Deltonerne 1,3,5 og 7 (eller 4, 5, 6 og 7) danner en durseptimakkord. Langt oppe i rækken finder vi en moltreklang: deltone nr. 10, 12 og 15. Imidlertid er der et tydeligt durpræg over overtonerækken, i og med at durtreklangen ligger på nogle lave og derfor normalt kraftige deltoner.
Flageolettoner
På et strygeinstrument kan man danne overtonerækken medflageoletter ved at lade strengen klinge i sin helhed, strejfe strengen midtvejs for at få 2. deltone, strejfe den en tredjedel inde for at få 3. deltone, etc. De steder, man kan strejfe strengen er i nodeeksemplet vist med en kantet node, mens den klingende node er vist med sort nodehoved:
Tilsvarende kan man "blæse over" på et blæseinstrument. Lyt til de første 16 deltoner fra det dybe G og læg mærke til, hvor tonehøjden er overraskende lav eller høj i forhold til ligesvævende temperatur - den lave septim f. eks., som Nørgård ofte udnytter. Musikeksemplet afsluttes med en G-dur treklang dannet af 4 deltoner - læg mærke til, hvor velgørende det er at høre enfuldstændig ren treklang.
Åbent hierarki
Overtonerækken danner et åbent hierarki , for hver af tonerne i den er udgangspunkt for en ny overtonerække, der faktisk er indeholdt i rækken. Fra den 2. deltone G2 kan man således tage hver anden tone ud og få en ny overtonerække på G2. Fra D3 kan man tage hver tredje tone ud og få en ny overtonerække på D. Ligeledes fra H3 og F4.
Det oprindelige spektrum fra G1 kunne i virkeligheden være en del af et endnu dybere spektrum. Altså, ingen top, ingen bund.
________________________________________________________________________
PA-højttaler :
________________________________________________________________________
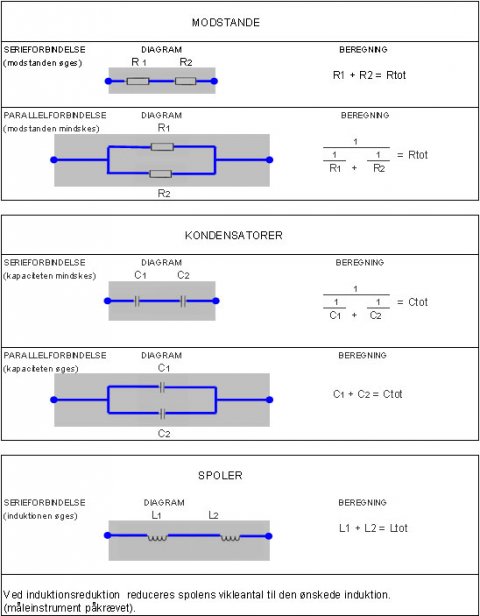
Parallel- og serieforbindelser :
________________________________________________________________________
Passiv højttaler : Højttalersystem uden indbygget forstærker.
________________________________________________________________________
________________________________________________________________________
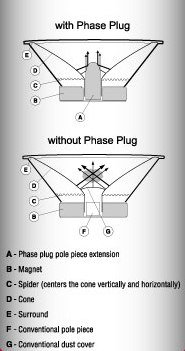
Phase Plug :
_______________________________________________________________________
Phon : Equal-loudness contour er betegnelsen for lydtryk ( dB SPL ) over et frekvens spektrum, som en lytter opfatter som en konstant lydstyrke, når det præsenteres med rene konstante toner.
Måleenhed for lydstyrkeniveauer læses i phon med henvisning til equal-loudness contours. Pr. definition siges at to sinus bølger med forskellige frekvenser, har equal-loudness niveau målt i PHONS hvis de opfattes som lige så højt som en gennemsnitlig hørelse (yngre person).
Equal-loudness konturer er ofte benævnt "Fletcher-Munson" kurver, efter de tidligste forskere, men disse undersøgelser er blevet afløst og indarbejdet i nyere standarder. De endelige kurver er defineret i den internationale standard ISO 226:2003.
________________________________________________________________________
Pink Noise : - kædes ofte sammen med White Noise, hvilket er nærliggende, idet begge signaltyper indeholder samtlige frekvenser i et kontinuertligt tidsforløb og et givet frekvensområde, typisk 20-20.000 Hz (høres som sus). Signalet frembringes elektrisk af en tonegenarator.
Forskellen mellem de to signaltyper findes i fordelingen af energimængden.
White Noise har konstant energimængde pr. Hz, - eksempelviser er der lige stor energimængde mellem 20 og 21 Hz som mellem 2000 og 2001 Hz.
Frekvenskurven for White Noise er lineær.
Oktav-inddeler man frekvensområdet 20-20.000 Hz (én oktav er pr. difinitation en fordobling af frekvensen) vil man se følgende opdeling med tilsvarende faktor for energiindhold i rød parantes.
én oktav = 20 - 40 Hz (20)
én oktav = 40 - 80 Hz (40)
én oktav = 80 - 160 Hz (80)
én oktav = 160 - 320 Hz (160)
én oktav = 320 - 640 Hz (320)
én oktav = 640 - 1280 Hz (640)
én oktav = 1280 - 2560 Hz (1280)
én oktav = 2560 - 5120 Hz (2560)
én oktav = 5120 - 10240 Hz (5120)
én oktav = 10240 - 20480 Hz (10240)
I Spectrum Analyzere (SPA) og Realtime Analyzere (RTA) målemetoder anvendes oktavinddelte måleintervaller, hvilket kræver en ensartet energifordeling af målesignalet pr oktav.
I Pink Noise signaltypen sænkes energimængden pr. oktav ved stigende frekvens for at opnå korrekte målinger.
Frekvenskurven for Pink Noise er faldende med stigende frekvens.
________________________________________________________________________
Port :
________________________________________________________________________
Propagation delay :
Propagation delay is a technical term that can have a different meaning depending on the context. It can relate to networking, electronics or physics. In general it is the length of time taken for the quantity of interest to reach its destination. Contents 1 Networking 2 Electronics 3 Physics
Networking :
In computer networks, propagation delay is the amount of time it takes for the head of the signal to travel from the sender to the receiver. It can be computed as the ratio between the link length and the propagation speed over the specific medium. Propagation delay is equal to d / s where d is the distance and s is the wave propagation speed. In wireless communication, s=c, i.e. the speed of light. In copper wire, the speed s generally ranges from .59c to .77c. This delay is the major obstacle in the development of high-speed computers and is called the interconnect bottleneck in IC systems.
Electronics :
A full adder has an overall gate delay of 3 logic gates from the inputs A and B to the carry output Cout shown in red In electronics, digital circuits and digital electronics, the propagation delay, or gate delay, is the length of time which starts when the input to a logic gate becomes stable and valid to change, to the time that the output of that logic gate is stable and valid to change. Often on manufacturers' datasheets this refers to the time required for the output to reach 50% of its final output level when the input changes to 50% of its final input level. Reducing gate delays in digital circuits allows them to process data at a faster rate and improve overall performance. The difference in propagation delays of logic elements is the major contributor to glitches in asynchronous circuits as a result of race conditions. The principle of logical effort utilizes propagation delays to compare designs implementing the same logical statement. Propagation delay increases with operating temperature, marginal supply voltage as well as an increased output load capacitance. The latter is the largest contributor to the increase of propagation delay. If the output of a logic gate is connected to a long trace or used to drive many other gates (high fanout) the propagation delay increases substantially. Wires have an approximate propagation delay of 1 ns for every 6 inches (15 cm) of length. Logic gates can have propagation delays ranging from more than 10 ns down to the picosecond range, depending on the technology being used.
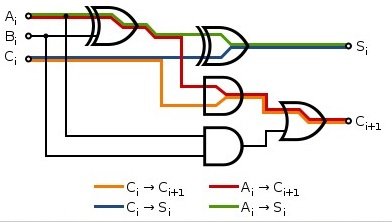
A full adder has an overall gate delay of 3 logic gates from the inputs A and B to the carry output Cout shown in red
_______________________________________________________________________